رمزگذاری اطلاعات قبل از انتقال برای اطمینان از امنیت داده ها و تحویل کارآمد اطلاعات ضروری است. برنامه MATLAB ارائه شده در اینجا اطلاعات را رمزگذاری و رمزگشایی می کند و همچنین مقادیر آنتروپی، کارایی و فرکانس احتمالات کاراکترهای موجود در جریان داده را مشخص می کند.
الگوریتم هافمن یک روش رمزگذاری محبوب است که در سیستم های ارتباطی الکترونیکی استفاده می شود. این به طور گسترده در همه فرمت های فشرده سازی اصلی که ممکن است با آنها روبرو شوید - از GZIP، PKZIP (winzip و غیره) و BZIP2 گرفته تا فرمت های تصویری مانند JPEG و PNG استفاده می شود. برخی از برنامه ها فقط از روش کدگذاری هافمن استفاده می کنند، در حالی که برخی دیگر از آن به عنوان یک مرحله در فرآیند فشرده سازی چند مرحله ای استفاده می کنند. (لازم به ذکر است در حامی ورکس پروژه متلب زیادی در این خصوص انجام شده است)
الگوریتم کدگذاری و تصمیم گیری هافمن در فشرده سازی داده ها با کدهای با طول متغیر استفاده می شود. کوتاه ترین کدها به پرتکرارترین کاراکترها و طولانی ترین کدها به کاراکترهای نادر اختصاص داده می شوند.
کدگذاری هافمن یک الگوریتم رمزگذاری آنتروپی است که برای فشرده سازی داده ها بدون خطا استفاده می شود. آنتروپی معیاری برای پیش بینی ناپذیری یک جریان اطلاعات است. حداکثر آنتروپی زمانی رخ می دهد که یک جریان داده دارای بیت های کاملاً غیرقابل پیش بینی باشد. یک جریان کاملاً ثابت از بیت ها (همه صفرها یا همه یک ها) کاملاً قابل پیش بینی است (آنتروپی ندارد).
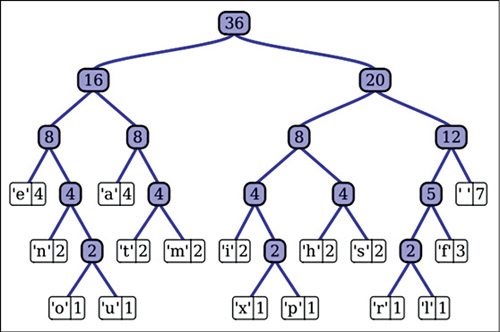
شکل 1. درخت هافمن
روش کدگذاری هافمن تا حدودی شبیه به روش شانون-فانو است. تفاوت اصلی بین این دو روش این است که شانون-فانو کدهای خود را از بالا به پایین می سازد (و بیت های هر کلمه رمز از چپ به راست ساخته می شوند)، در حالی که هافمن یک درخت کد از پایین به بالا و بیت های هر کلمه از راست به چپ ساخته می شوند.
مدل درخت هافمن در اینجا در شکل نشان داده شده است و با استفاده از الگوریتم هافمن تولید می شود. اینجا درخت 36 شاخه دارد. در زیر گره شاخه می توانید گره های برگ 16 و 20 را مشاهده کنید. با اضافه کردن 16 و 20 عدد 36 به دست می آید. با افزودن 8 و 8 عدد 16 به دست می آید در حالی که 4+4=8 است. در سمت چپ، 'e' به 4 متصل است. به طور مشابه، 'a'، 'n'، 't' و غیره برای تشکیل درخت هافمن کامل وصل شده اند.
برای جزئیات در مورد تشکیل درخت هافمن، لطفاً به پروژه نرم افزاری «فشرده سازی و رفع فشار داده» که در EFY آوریل 2005 منتشر شده است مراجعه کنید.
ساده ترین الگوریتم ساخت درخت از یک صف استفاده می کند که در آن گره با کمترین احتمال یا فرکانس بالاترین اولویت را دارد.
ابتدا یک گره برگ برای هر نماد یا کاراکتر ایجاد کنید و آن را به جدول اولویت اضافه کنید. اگر بیش از یک گره در جدول وجود دارد، دو گره با بالاترین اولویت (کمترین فرکانس) را از جدول حذف کنید. یک گره جدید با این دو گره به عنوان گره فرعی و با احتمال برابر با مجموع احتمالات دو گره ایجاد کنید. به همین ترتیب ادامه دهید تا به آخرین گره واحد برسید. آخرین گره ریشه است، بنابراین درخت اکنون کامل است.
پیشنهاد میکنم مقاله "معرفی بهترین کتاب های آموزش متلب" مطالعه کنید.
مراحل رمزگذاری داده ها با استفاده از کدگذاری هافمن
- مرحله 1. احتمال هر کاراکتر را در مجموعه ای از داده ها محاسبه کنید.
- مرحله 2. مجموعه داده ها را به ترتیب صعودی مرتب کنید.
- مرحله 3. یک گره جدید ایجاد کنید که در آن گره فرعی سمت چپ کمترین فرکانس را در لیست مرتب شده و گره فرعی سمت راست دومین کمترین فرکانس در لیست مرتب شده باشد.
- مرحله 4. این دو عنصر را از لیست مرتب شده حذف کنید زیرا اکنون بخشی از یک گره هستند و احتمالات را اضافه کنید. نتیجه احتمال گره جدید است.
- مرحله 5. مرتب سازی را در لیست انجام دهید.
- مرحله 6. مراحل 3، 4 و 5 را تکرار کنید تا زمانی که تنها یک گره باقی بماند.
اکنون که یک گره باقی مانده است، به سادگی درخت را رسم کنید.
با درخت فوق، در هر مسیری که به سمت چپ میرود یک عدد 0 و در هر مسیری که به سمت راست میرود یک عدد 1 قرار دهید. اکنون با شمارش 0 و 1 از ریشه، کد باینری را به هر یک از نمادها یا کاراکترها اختصاص دهید.
از آنجایی که ساختارهای داده اولویت صف کارآمد به زمان O(log n) در هر درج نیاز دارند، و درختی با برگ 'n' دارای 2n-1 گره است، این الگوریتم در زمان O(n log n) عمل می کند، جایی که 'n' عدد است.
با توجه به موارد فوق، اکنون مشخص است که روش رمزگذاری باید یک کد منحصر به فرد قابل رمزگشایی ایجاد کند تا پیام اصلی به طور منحصر به فرد و بدون خطا شناسایی شود. پیامی که با بیشترین احتمال تولید می شود، تعداد دفعات بیشتری نسبت به سایر پیام ها تولید می شود. در چنین حالتی، اگر از یک کد با طول متغیر به جای کد با طول ثابت استفاده کنید، با اختصاص بیت های کمتری به پیام های با احتمال بالاتر نسبت به پیام های با احتمال کمتر، کارایی را بهبود می بخشید.
نحوه کار برنامه متلب
- احتمالات منبع را به ترتیب کاهشی فهرست کنید.
- احتمالات دو نماد را که کمترین احتمال را دارند ترکیب کنید و احتمالات حاصل را ثبت کنید. این مرحله کاهش نامیده می شود. این روش تا زمانی که احتمالات دو مرتبه باقی بماند تکرار می شود.
- رمزگذاری را با آخرین کاهش که دقیقاً از احتمالات دو مرتبه تشکیل شده است، شروع کنید. "0" را به عنوان اولین رقم در کلمات رمز برای همه نمادهای منبع مرتبط با احتمال اول اختصاص دهید. "1" را به احتمال دوم اختصاص دهید.
- اکنون به عقب برگردید و برای دو احتمالی که در مرحله کاهش قبلی با هم ترکیب شده بودند، "0" و "1" را به رقم دوم اختصاص دهید، و تمام تخصیص های انجام شده در مرحله 3 را حفظ کنید.
- به این ترتیب کاهش را تا رسیدن به ستون اول ادامه دهید.
- آنتروپی را محاسبه کنید. آنتروپی کد میانگین تعداد بیت های مورد نیاز برای رمزگشایی یک الگوی معین است.
- محاسبه بهره وری را برای ارزیابی کد منبع تولید شده، باید کارایی آن را محاسبه کنید.
کارایی = آنتروپی (H(X))/میانگین طول کلمه رمز (N)
میانگین طول کلمه رمز توسط:
N =∑ (Pi × Ni)
که در آن Ni طول کلمه رمز یکم و Pi احتمال وقوع است.
توابع متلب
هافماننکو. این تابع در کدنویسی هافمن استفاده می شود. نحو عبارت است از:
comp = huffmanenco(sig,dict)
این خط سیگنال "sig" توصیف شده توسط فرهنگ لغت "dict" را رمزگذاری می کند. آرگومان 'sig' می تواند به شکل یک بردار عددی، آرایه سلول عددی یا آرایه سلولی الفبایی باشد. اگر "sig" یک آرایه سلولی است، باید یک ردیف یا یک ستون باشد. «dict» یک آرایه سلولی Nx2 است که در آن «N» تعداد نمادهای ممکن متمایز برای کدگذاری است. ستون اول «dict» نمادهای متمایز و ستون دوم نشان دهنده کلمات رمز مربوطه است. هر کلمه رمز به عنوان یک بردار ردیف عددی نشان داده می شود و هیچ کلمه رمزی در "dict" نمی تواند پیشوند هر رمز دیگری در "dict" باشد. با استفاده از تابع huffmandict می توانید "dict" را تولید کنید.
هافماندکو این تابع در رمزگشایی هافمن استفاده می شود. عبارت است از:
dsig = huffmandeco(comp,dict)
این خط بردار کد هافمن عددی را با استفاده از فرهنگ لغت کد 'dict' رمزگشایی می کند. آرگومان 'dict' یک آرایه سلولی Nx2 است، که در آن 'N' تعداد نمادهای ممکن متمایز در سیگنال اصلی است که به عنوان 'comp' کدگذاری شده است. ستون اول «dict» نمادهای متمایز و ستون دوم نشان دهنده کلمات رمز مربوطه است. هر کلمه رمز به عنوان یک بردار ردیف عددی نشان داده می شود و هیچ کلمه رمزی در "dict" مجاز نیست پیشوند هر رمز دیگری در "dict" باشد. با استفاده از تابع Huffmandict میتوانید «dict» و با استفاده از تابع huffmanenco ,comp ایجاد کنید. اگر همه مقادیر سیگنال در "dict" عددی باشند، "dsig" یک بردار است. اگر هر مقدار سیگنال در "dict" الفبایی باشد، "dsig" یک آرایه سلولی یک بعدی است.
پیشنهاد میکنم مقاله "20 ایده برتر برای پروژه متلب" مطالعه کنید.
آزمایش کردن
- برنامه MATLAB را اجرا کنید. این برنامه ابتدا فرهنگ لغت پیام ها را تولید می کند. این پیامها چیزی جز کدها یا جریانهای بیتی از 00 تا 1001 در این مثال نیستند. شما می توانید این محدوده را با تغییر در کد منبع گسترش دهید. خروجی برنامه MATLAB برای مثال در زیر آورده شده است:
احتمالات را وارد کنید:
[0.3 0.25
0.2 0.12 0.08 0.05]
کد هافمن دستور می دهد:
[1] '0 0'
[2] '0 1'
[3] "1 1"
[4] "1 0 1"
[5] "1 0 0 0"
[6] '1 0 0 1'
علامت ها را بین 1 تا 6 وارد کنید.
sym = 3
خروجی کدگذاری شده:
1 1
جریان بیت را در [1 1] وارد کنید.
نمادها عبارتند از: 3
آنتروپی 2.360147 بیت است.
بازده 0.991659 است.
m = 4
s = 2
واریانس: 2
- ابتدا، برنامه از شما می خواهد که عدد بین «1» و «6» را وارد کنید. وقتی "3" را وارد می کنید، کد "1 1" روی صفحه ظاهر می شود. این کد چیزی نیست جز کاراکتر مربوط به عدد "3". از این رو رمزگذاری با موفقیت انجام می شود.
- برای رمزگشایی، بیت استریم "1 1" را وارد کنید. خروجی تولید شده "3" است.
- به جای «3»، میتوانید از ترکیبهای مختلف از «1» تا «6» استفاده کنید.

این برنامه مقادیر حداکثر طول (m) و حداقل طول (s) تولید شده در فرهنگ لغت را خروجی می دهد. حداکثر طول تولید شده "1111" است، یعنی m=4. حداقل طول "00" است که دو بیت طول دارد و بنابراین s=2 است.
به کدگذاری هافمن، کدگذاری حداقل واریانس نیز گفته می شود. واریانس حداکثر طول-حداقل طول است. بنابراین واریانس در این مثال "2" است.
برای دانلود منبع کد پروژه کدگذاری و رمزگشایی هافمن در متلب اینجا کلیک کنید
ثبت پروژه جدید
پروژه ای برای انجام داری؟
تخصص انجام پروژه داری؟



دیدگاه خود را بیان کنید
1000 کاراکتر باقیمانده است